广度优先搜索

广度优先搜索算法（Breadth-First Search，缩写为 BFS），又称为宽度优先搜索，是一种图形搜索算法。简单的说，BFS 是从根结点开始，沿着树的宽度遍历树的结点。如果所有结点均被访问，则算法中止。

例题

102 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1： 输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]]

示例 2：

输入： root = [1] 输出： [[1]]

示例 3：

输入： root = [] 输出： []

提示：

树中节点数目在范围 [0, 2000] 内
$-1000 <= Node.val <= 1000$

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func levelOrder(root *TreeNode) [][]int {
    result := [][]int{}

    if root == nil {
        return result
    }
    // 队列
    queue := []*TreeNode{root}
    for len(queue) != 0 {
        row := []int{}
        for n := len(queue); n > 0; n-- {
            temp := queue[0]
            row = append(row, temp.Val)
            // 出队
            queue = queue[1:]
            // 子节点入队
            if temp.Left != nil {
                queue = append(queue, temp.Left)
            }
            if temp.Right != nil {
                queue = append(queue, temp.Right)
            }
        }
        result = append(result, row)
    }
    return result
}

733 图像渲染

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。

你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行上色**填充** 。

为了完成** 上色工作** ，从初始像素开始，记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为 newColor 。

最后返回经过上色渲染后的图像。

示例 1:

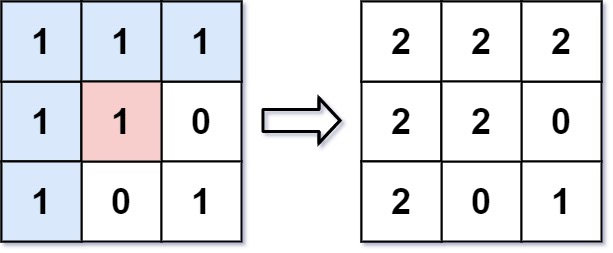
输入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间，(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。

示例 2:

输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2 输出: [[2,2,2],[2,2,2]]

提示:

m == image.length
n == image[i].length
1 <= m, n <= 50
0 <= image[i][j], newColor < 216
0 <= sr <m
0 <= sc <n

func floodFill(image [][]int, sr int, sc int, color int) [][]int {
    dir := [][]int{
        {-1, 0},
        {1, 0},
        {0, -1},
        {0, 1},
    }
    origin := image[sr][sc]
    if origin == color {
        return image
    }
    // 初始化队列
    queue := [][]int{{sr, sc}}
    for len(queue) > 0 {
        pos := queue[0]
        currX := pos[0]
        currY := pos[1]

        for _, v := range dir {
            // 如果四个方向像素相连，入队
            nextX := pos[0] + v[0]
            nextY := pos[1] + v[1]
            if isPos(image, nextX, nextY) && image[nextX][nextY] != -1 && image[nextX][nextY] == origin {
                image[nextX][nextY] = -1
                queue = append(queue, []int{nextX, nextY})
            }
        }
        // 填色，出队
        image[currX][currY] = color
        queue = queue[1:]
    }
    return image
}

func isPos(image [][]int, x int, y int) bool {
    if x >= 0 && x < len(image) && y >= 0 && y < len(image[0]) {
        return true
    }
    return false
}

695 岛屿大小

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 **水平或者竖直的四个方向上 ** 相邻。你可以假设 grid 的四个边缘都被 0 （代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

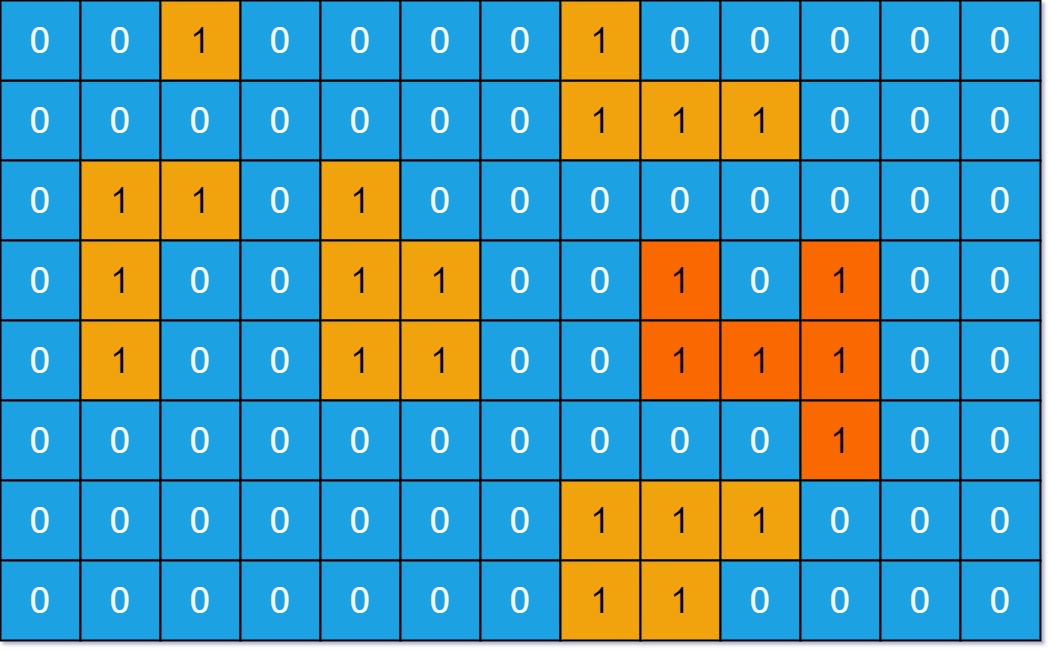
输入： grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出： 6 解释： 答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入： grid = [[0,0,0,0,0,0,0,0]] 输出： 0

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

func maxAreaOfIsland(grid [][]int) int {
    result := 0

    for i, row := range grid {
        for j, v := range row {
            if v == 1 {
                temp := search(grid, i, j)
                if result < temp {
                    result = temp
                }
            }
        }
    }
    return result
}

func search(grid [][]int, x int, y int) int {
    result := 0
    dir := [][]int{
        {-1, 0},
        {1, 0},
        {0, -1},
        {0, 1},
    }

    // 初始化队列
    queue := [][]int{{x, y}}
    for len(queue) > 0 {
        pos := queue[0]
        currX := pos[0]
        currY := pos[1]

        for _, v := range dir {
            // 如果四个方向像素相连，入队
            nextX := currX + v[0]
            nextY := currY + v[1]
            grid[currX][currY] = -1
            if isPos(grid, nextX, nextY) && grid[nextX][nextY] == 1 {
                grid[nextX][nextY] = -1
                queue = append(queue, []int{nextX, nextY})
            }
        }

        result++
        queue = queue[1:]
    }
    return result
}

func isPos(image [][]int, x int, y int) bool {
    if x >= 0 && x < len(image) && y >= 0 && y < len(image[0]) {
        return true
    }
    return false
}

116 填充每个节点的下一个右侧节点指针

给定一个**完美二叉树** ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有next 指针都被设置为 NULL 。

示例 1：

输入： root = [1,2,3,4,5,6,7] 输出： [1,#,2,3,#,4,5,6,7,#] 解释： 给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入： root = [] 输出： []

提示：

树中节点的数量在 [0, 212- 1] 范围内
-1000 <= node.val <= 1000

进阶：

*你只能使用常量级额外空间。
*使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    // 以 nil 作为每一层的分割点，如果检测到 nil 重置队列
    queue := []*Node{root, nil}
    for {
        for i, v := range queue {
            if v == nil {
                // 链接
                queue[i-1].Next = nil
                // 出队
                queue = queue[i+1:]
                queue = append(queue, nil)
                break
            } else {
                // 链接
                v.Next = queue[i+1]
            }

            // 入队
            if v.Left != nil && v.Right != nil {
                queue = append(queue, v.Left)
                queue = append(queue, v.Right)
            }
        }

        // 中止
        if queue[0] == nil {
            break
        }
    }
    return root
}

💣 542 01 矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

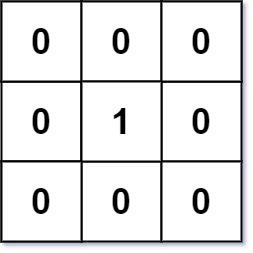
输入： mat = [[0,0,0],[0,1,0],[0,0,0]] 输出： [[0,0,0],[0,1,0],[0,0,0]]

示例 2：

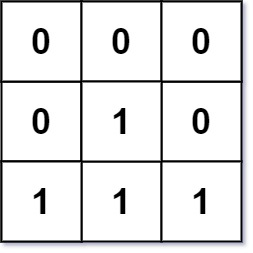
输入： mat = [[0,0,0],[0,1,0],[1,1,1]] 输出： [[0,0,0],[0,1,0],[1,2,1]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

func updateMatrix(matrix [][]int) [][]int {

    n, m := len(matrix), len(matrix[0])
    queue := make([][]int, 0)
    for i := 0; i < n; i++ {    // 把0全部存进队列，后面从队列中取出来，判断每个访问过的节点的上下左右，直到所有的节点都被访问过为止。
        for j := 0; j < m; j++ {
            if matrix[i][j] == 0 {
                point := []int{i, j}
                queue = append(queue, point)
            } else {
                matrix[i][j] = -1
            }
        }
    }
    direction := [][]int{
        {0, 1},
        {0, -1},
        {1, 0},
        {-1, 0}
    }

    for len(queue) > 0 {  // 这里就是 BFS 模板操作了。
        point := queue[0]
        queue = queue[1:]
        for _, v := range direction {
            x := point[0] + v[0]
            y := point[1] + v[1]
            if x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] == -1 {
                matrix[x][y] = matrix[point[0]][point[1]] + 1
                queue = append(queue, []int{x, y})
            }
        }
    }

    return matrix
}

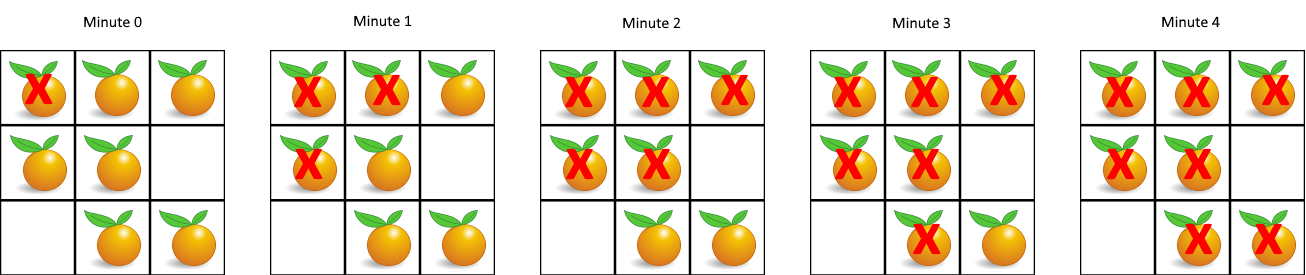
994 腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子**周围4 个方向上相邻** 的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1：

输入： grid = [[2,1,1],[1,1,0],[0,1,1]] 输出： 4

示例 2：

输入： grid = [[2,1,1],[0,1,1],[1,0,1]] 输出： -1 解释： 左下角的橘子（第 2 行，第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

输入： grid = [[0,2]] 输出： 0 解释： 因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0 、 1 或 2

func orangesRotting(grid [][]int) int {
    queue := [][]int{}
    for i, row := range grid {
        for j, v := range row {
            if v == 2 {
                queue = append(queue, []int{i,j})
            }
        }
    }

    result := search(grid, queue)

    for _, row := range grid {
        for _, v := range row {
            if v == 1 {
                return -1
            }
        }
    }
    return result
}

var dirs = [][]int{
    {-1, 0},
    {1, 0},
    {0, -1},
    {0, 1},
}

func search(grid [][]int, queue [][]int) int {
    result := 0

    for len(queue) > 0 {
        tempQueue := [][]int{}
        n := len(queue)
        for i := 0; i < n; i++ {
            currX := queue[i][0]
            currY := queue[i][1]

            for _, v := range dirs {
                nextX := currX + v[0]
                nextY := currY + v[1]

                if isPos(grid, nextX, nextY) && grid[nextX][nextY] == 1 {
                    grid[nextX][nextY] = 2
                    tempQueue = append(tempQueue, []int{nextX, nextY})
                }
            }

            if i == len(queue) - 1 {
                queue = tempQueue
            }
        }

        if len(queue) > 0 {
            result++
        }
    }
    return result
}

func isPos(image [][]int, x int, y int) bool {
    if x >= 0 && x < len(image) && y >= 0 && y < len(image[0]) {
        return true
    }
    return false
}